Manifold-Manifold Distance with Application to
Face Recognition based on Image Set
Ruiping
Wang1, Shiguang Shan1, Xilin Chen1, Wen Gao2
1Key Lab of
Intelligent Information Processing,
2School of
EE&CS,
|
|
|
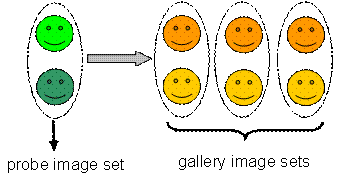
Face Recognition based on
Image Set (FRIS) |
Abstract - In this paper, we address the
problem of classifying image sets, each of which contains images belonging to
the same class but covering large variations in, for instance, viewpoint and
illumination. We innovatively formulate the problem as the computation of
Manifold-Manifold Distance (MMD), i.e., calculating the distance between
nonlinear manifolds each representing one image set. To compute MMD, we also
propose a novel manifold learning approach, which expresses a manifold by a
collection of local linear models, each depicted by a subspace. MMD is then
converted to integrating the distances between pair of subspaces respectively
from one of the involved manifolds.
The proposed MMD method is evaluated on the task of
Face Recognition based on Image Set (FRIS). In FRIS, each known subject is
enrolled with a set of facial images and modeled as a gallery manifold, while a
testing subject is modeled as a probe manifold, which is then matched against
all the gallery manifolds by MMD. Identification is achieved by seeking the
minimum MMD. Experimental results on two public face databases, Honda/UCSD and
CMU MoBo, demonstrate that the proposed MMD method outperforms the competing
methods.
Publication:
Manifold-Manifold Distance with Application to Face Recognition
based on Image Set
Ruiping Wang, Shiguang Shan, Xilin Chen and Wen Gao
IEEE Conference on Computer Vision and Pattern Recognition (CVPR),
Anchorage, Alaska, June 24-26, 2008. [paper]
Motivation
|
|
|
|
Traditional recognition task |
Object Recognition based on Image Set (ORIS) |
Problem Formulation
Ø
For visual object
recognition, patterns can be represented in three possible levels:
n
Point (P): individual
sample
n
Subspace (S): linear
model spanned by some samples
n
Manifold (M): nonlinear
low-dimensional embedding learned from a large number of samples
Ø
In some sense, the core
of pattern classification is the distance computation among the three
representations.
|
|
|
|
|
|
|
|
|
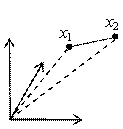
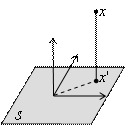
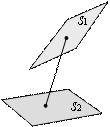
point to point |
point to subspace distance (PSD) |
subspace to subspace distance (SSD) |
|
point to manifold distance (PMD) |
subspace to manifold distance (SMD) |
manifold to manifold distance (MMD) |
Manifold to Manifold Distance (MMD)
Ø
Basic ideas
n
Manifold can be modeled
by a collection of local linear subspaces.
n
The distances associated
with manifold can be converted to those defined on subspaces.
n
Formally, we denote the
component subspaces of a manifold M by Ci , and express a manifold as:
![]()
Ø
Our approach
n
MMD is converted to the
integration of distances between pair of subspaces.
n
For the ORIS task, the
most effective solution is to find the common views and measure the similarity
of those parts of data.
n
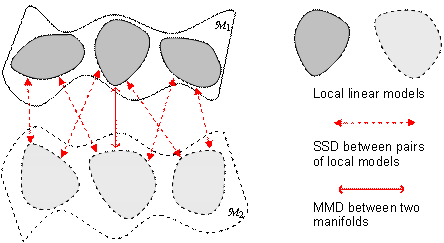
Therefore, we define MMD
by the closest subspace pair from the two manifolds.
![]()
|
|
|
Conceptual illustration |
Ø
Discussion
n
We measure the similarity
between two manifolds by the similarity between their best suited local models.
n
While many others may be
explored, however, for the ORIS task, our definition is believed to be one of
the most appropriate.
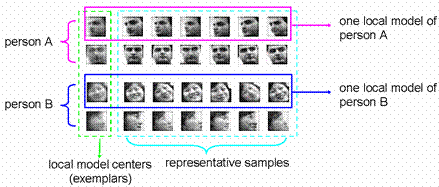
Local linear model construction
Ø
Maximal Linear Patch (MLP)
n
Linear criterion: geodesic distance is as close to
Euclidean distance as possible in the patch, which guarantees the near
linearity of the patch.
n
Maximal criterion: the patch size is maximized such
that any appending of additional data point would violate the linear criterion.
n
Each MLP is then
characterized by a linear subspace using PCA.
Ø
One-shot algorithm to
construct MLPs
n
Basic idea: each new MLP
is stemmed from a seed point gradually until the linear constraint is broken.
|
|
|
|
|
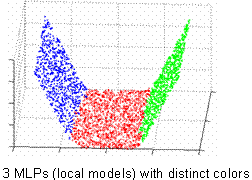
Illustration of MLP on a toy example |
Local models constructed from real face dataset |
|
Local linear model distance
For two subspaces ![]() and
and ![]()
Ø
Denote their exemplars
by: ![]() ,
, ![]() , and bases by:
, and bases by: ![]() ,
, ![]() .
.
Ø
Define variation distance measure by the
average of canonical correlations:
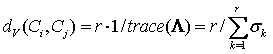
Ø
Define exemplar distance measure by the correlation
of the two exemplars:
![]()
Ø
Our definition of SSD
(local linear model distance):
![]() , (
, (![]() is a weight parameter)
is a weight parameter)
|
|
|
Local model similarity by using our definition of
SSD |
Experimental Results
Ø
Experimental setting on FRIS
n
Each known subject
(enrolled with a set of images) is modeled as a gallery manifold.
n
A testing subject is
modeled as a probe manifold, which is then matched against all the
gallery manifolds by MMD.
n
Identification is
achieved by seeking the minimum MMD.
Ø
Datasets
|
|
|
|
Examples from Honda/UCSD |
Examples from CMU MoBo |
|
Table 1. Two public datasets for FRIS task |
|||
|
Database |
Persons |
Videos |
Image Size |
|
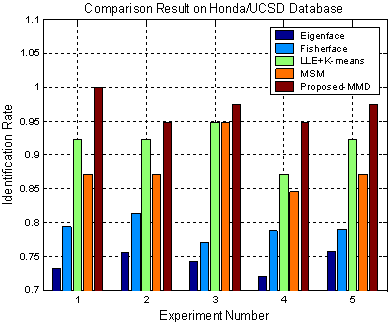
Honda/UCSD |
20 |
59 |
20*20 |
|
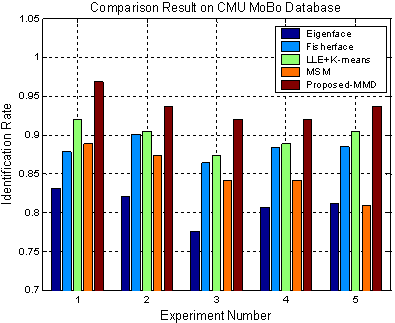
CMU MoBo |
25 |
100 |
30*30 |
Ø
Comparative methods
n
Nearest neighbor (NN)
matching in (i) Eigenface, and (ii) Fisherface,
n
NN matching in LLE + k-means clustering, which is a
typical exemplar-based method,
n
Mutual Subspace Method (MSM), which is a typical variation-based
method,
n
The proposed MMD
method.
Ø
Identification results
|
|
|
Conclusion
Ø
We formally and
explicitly formulate the ORIS task as the computation of what we name manifold to
manifold distance (MMD).
Ø
We propose a formal
definition of MMD, and present several technical contributions for its
computation, i.e.,
n
The local linear model
construction method
n
A more effective subspace
distance measure definition.
Ø
The proposed MMD method
is applied to Face Recognition with Image Set (FRIS) problem, and impressive
results are achieved.